Now, this is a story all about how
My language network cycled back roundWill Smith
Language is rich with many examples of different words being used to describe the same idea, and the same word to describe different ideas. Can you think of any such examples?
Suppose that we want to teach a language to machines. There exist many clever machine learning algorithms by which computers process words to create and convey ideas. This usually involves some initial human input, so we are not interested in this type of learning. Rather, the question we are asking is: do computers possess the ability to learn a language the same way children do — from scratch?
To answer this question we must first establish how learning takes place. Natural languages can be learnt, as well as taught, using two distinct approaches through either inductive learning (the act of discovery) or deductive learning (the act of reasoning). We as human beings are the only species that can learn or can acquire knowledge using both approaches, and through integration of shared features between the two we acquire new words [1].
For instance, a child is taught through observation to recognise birds from an early age, a type of inductive learning. When the child grows up they may begin to identify new breeds of bird through deductive learning methods, such as reading scientific papers.
Machines cannot perform inductive reasoning simply on their own. Instead, human input is necessary so that computers are able to learn how to distinguish between logical and comical conclusions. It is so that computers do not confuse the word turkey, in the context of bird species, with either the country or a type of schnitzel, and vice-versa.
We hope that eventually a computer would be able to recognise these subtle differences without human input. What would then happen if a computer was instructed to learn an entire language simply by looking words up inside of a dictionary?
This is our chosen method for teaching language to computers – through dictionaries. After all, to understand a concept, one must also know the words used in the definition of this concept. However, transferring this learning technique to computers may cause infinite loops of self-referencing, which result from deductive learning.
This self-referencing mechanism is similar to a statement in set theory called Russell’s paradox. Because language is constantly evolving, at the moment new words are introduced their definitions can form loops of cross referencing. For example, does the word ‘indescribable’ stay true to its meaning or is it in fact ‘describable’? Is this a paradox? Coupled with the pursuit for simplicity in many computing disciplines, taking dictionaries in their current format is not an ideal approach for computers to learn a language.
Russell’s paradox, or: Naïve set theory is inconsistent. (Click to read the proof!)
Proof. Consider a set R with the property that its elements are all sets which are not members of themselves: R = {x | x ∉ x} Suppose that R ∈ R. Then by definition R does not contain itself as a member, i.e. R ∉ R. Conversely, suppose R ∉ R. Then R is a member of R because it holds all sets which are not members of itself. This shows that: R ∈ R ⇔ R ∉ R A contradiction therefore arises which implies inconsistency of naïve set theory. ◻
So far we have established that there is a difficulty in computers learning language using dictionary entries. What would then be an effective method for teaching computers?
Language is an interconnected network of words.
We can visualise the structure of a language as a network (also known as a directed graph). In this network, words are vertices and arrows point from a word to the words it is being defined with. Hence each dictionary entry pairs a given word (a) with several words (b,c,d) in the definition of word (a).
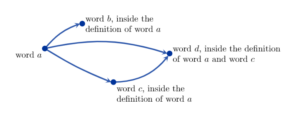
Since graphs showcase relationships in an elegant and quantifiable framework, we can begin to depict language as a network rather than as a listing of words in a dictionary.
By taking words and recursively exploring their definitions, we can construct paths from a word, to the definition of that word, to the definition of the words inside of its definition, and so on until we exhaust all words needed for defining a given concept [2, 3].
The illustration below illustrates how cycles may form in the directed graph of a language. This example graph contains four vertices, where each vertex represents a single word. The directed arrows are edges, pointing from one word to another word inside of its definition. Cycles are shown in blue, with larger cycles enclosing smaller cycles inside.
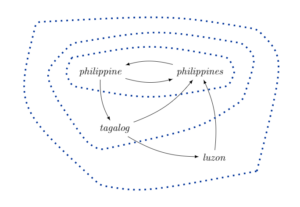
We find a cycle on vertices ‘luzon → philippines → philippine → tagalog → luzon’. This is because we can travel back to any starting vertex by following the directed edges in the cycle. And since this path also crosses the largest number of edges, it acts as the maximal cycle.
Another cycle exists on vertices ‘tagalog → philippines → philippine → tagalog’. Similarly, the path ‘philippine → philippines → philippine’ is the smallest cycle that exists. This is the circularity which computers fall into when learning words from a dictionary, and one we want to resolve.
What would circularity then look like inside a much larger language network? By identifying the nouns found in the English language, we build our final graph in the manner described above and using 5062 individual nouns. So naturally let’s call this the network of nouns graph. Details on the algorithms used to build such graphs can be found here.
An interesting structure emerges in this graph, in which we find 67 cycles, the largest of which encompasses 668 words. Examples of cycles are found in the table below, with shorter cycles showing meaningful connections between words and belonging to one topic [4].
|
|
|
|
By examining the topological features (shape and size) inside the network of nouns we can begin to answer the question on how cycles form.
One approach is to redesign dictionaries with a hierarchical tree structure in mind.
To help towards this, we want to imagine language as being a hierarchical tree (or acyclic graph), where each word must be learnt in order. Hierarchy means we start with one root word, from which the next word follows, until a list of all words has been learnt. Just as tree branches cannot grow back into the same root, new words cannot ever point to previously seen words inside this tree structure.
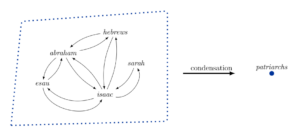
Condensing loops in language is one approach to designing such a tree structure. Start by identifying small cycles of words, where each word is associated with another on the basis that they have very similar meanings regarding a certain aspect. We can then categorise and condense these words into a single vertex on a quotient graph. This type of language optimisation helps to make computers less confused in our examples by removing cycles.
Consider the short cycle (definitional loop) consisting of five biblical names who had lived during the patriarchal age. It was found inside the network of nouns. To solve for this definitional loop we can condense the words into a single theme that encapsulates its universal essence, or to put plainly – a single word describing the topic ‘patriarchs’.
This cannot be made, for example, when decomposing the largest cycle inside the network of nouns, which shows no apparent association amongst the 668 words. Such large cycles pose an obstacle for machine’s ability to learn new concepts and extra tools are needed to explain and break large cycles down into smaller and more palatable loops.
One complication in teaching language to computers is due to homographic words.
These are words which are spelled the same and sound the same but have alternative meanings. They can often creep their way inside of definitional loops, causing edges to form between otherwise contrasting topics.

The way in which short definitional loops are detected is by following a rule that states: for a node to be included inside of a loop, it must comply with a threshold on the number of edges along a path from the word back to itself. If a node meets this criteria, it will be included inside a definitional loop. Examples of the shortest loops are shown below, with the maximum length of a path from every node back to itself noted besides each illustration.
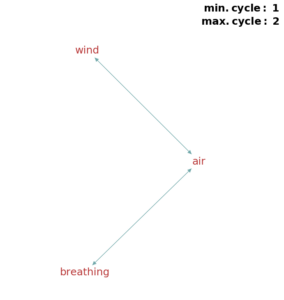 (a) Air movement. (a) Air movement. |
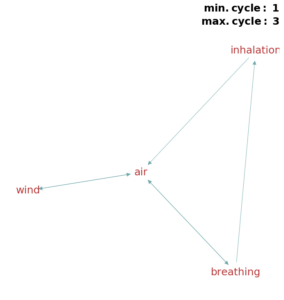 (b) Air movement and asthma. (b) Air movement and asthma. |
 (c) Biological system and work. (c) Biological system and work. |
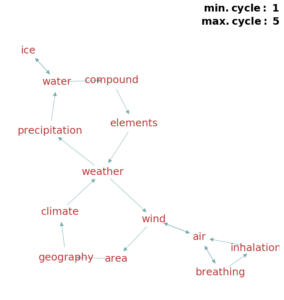 (d) Substances and weather system. (d) Substances and weather system. |
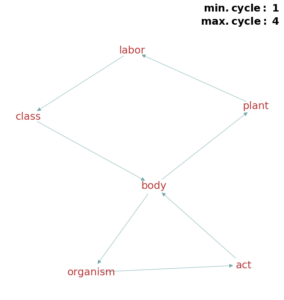
For example, we detect a definitional loop with maximum cycle length 4 belonging to the largest cycle inside the network of nouns:
body → organism → act → body → plant → labor → class → body
These words are found to have little etymological relevance with one another. It is feasible to assume that this is a topic which has to do with living structures. However, the edge ‘act → body’ relates to the administration of justice by a legislative body. Similarly, ‘body → plant’ depicting a biological system is misconstrued with the sense of the word for manufacturing, linking ‘plant → labor’.
Moreover, we attribute the bidirectional links (an edge which points in two directions) inside shorter cycles to what in linguistics is coined lexical meaning. Notice from the above example that words can possess several senses, an alternative set of word interpretations if you like. This pairing between different word senses in the design of language is what ultimately leads to unnecessary cycles to form.
As humans, we can often misconstrue a statement by using a word with the wrong semantic meaning and still be able to understand one another. This feature becomes amplified when machines are taught definitions absolutely and fall into circularity. It was shown how we can bring language to a more simplistic form by condensing a set of words into a single theme. Controlling language however, and its evolution therefore, can quickly turn tyrannical. After all, how would you feel if you were instructed not to use specific words? A balance is required if we are to create a process for teaching language from scratch whilst also allowing for its natural evolution.
Article by David Vichansky (MSc student of Mathematical Sciences at Utrecht University, the Netherlands)
References
[1] S. Harnad. From Sensorimotor Categories and Pantomime to Grounded Symbols and Propositions, 2011.
[2] A. Mass et al. How Is Meaning Grounded in Dictionary Definitions?, 2008.
[3] O. Picard et al. Hierarchies in Dictionary Definition Space, 2009.
[4] D. Levary et al. Loops and Self-Reference in the Construction of Dictionaries, 2012.
[5] S. Maslov et al. Specificity and Stability in Topology of Protein Networks, 2002.