The Dutch Travel Survey

In 2021 the Dutch population travelled a total distance of well over 150 billion kilometres within the Netherlands [1], or equivalently, about 187.000 round trips to the moon. To be able to construct and maintain the right infrastructure for all these travel movements, it is very important to have reliable data about the travel habits of the Dutch population.

The organization Statistics Netherlands (translated from the Dutch “Centraal Bureau voor de Statistiek”) has been tasked with collecting and analyzing this data, a project which has been named ODiN (“Onderweg in Nederland”, i.e. the Dutch Travel Survey). Statistics Netherlands is an autonomous administrative authority, which means that it performs public service tasks, but it is independent from and not under the direct authority of a Dutch ministry [2]. The aim of the ODiN project is to create a picture of the travel movements of the Dutch population as a whole. This means that it is not relevant which roads people take, but rather in what ways people travel. For example, the precise route you take to the shops is not important, but whether you go by car or by bike is. Some relevant properties of the travel movements are distance travelled, mode of transportation and number of stops.

For the predecessor of ODiN, participants were asked to write down on paper what they did and where they went during the day. For the ODiN project, participants were asked to track their location using an app for a couple of days. At the end of each day, they had to check if the data, and more importantly the mode of transportation that the app registered, was correct. Some screenshots of that app can be found in Figure 1.

An issue that occurs is the existence of so-called “gaps” in the location data, where a whole bunch of consecutive data points is missing. Each gap is a period of time in which no location data is collected. There are many reasons why we get such gaps: there might be a loss of connection when going through a tunnel or a bridge, the phone might shut down the app unexpectedly, or the phone could run out of battery.

The easiest way to fill such a gap is with a straight line, which is what Statistics Netherlands has been doing for years. However, this leads to errors that keep repeating themselves, like underestimating the distance travelled. As we can see in the example below, the straight red line is much shorter than the wonky path, which is the actual path travelled.

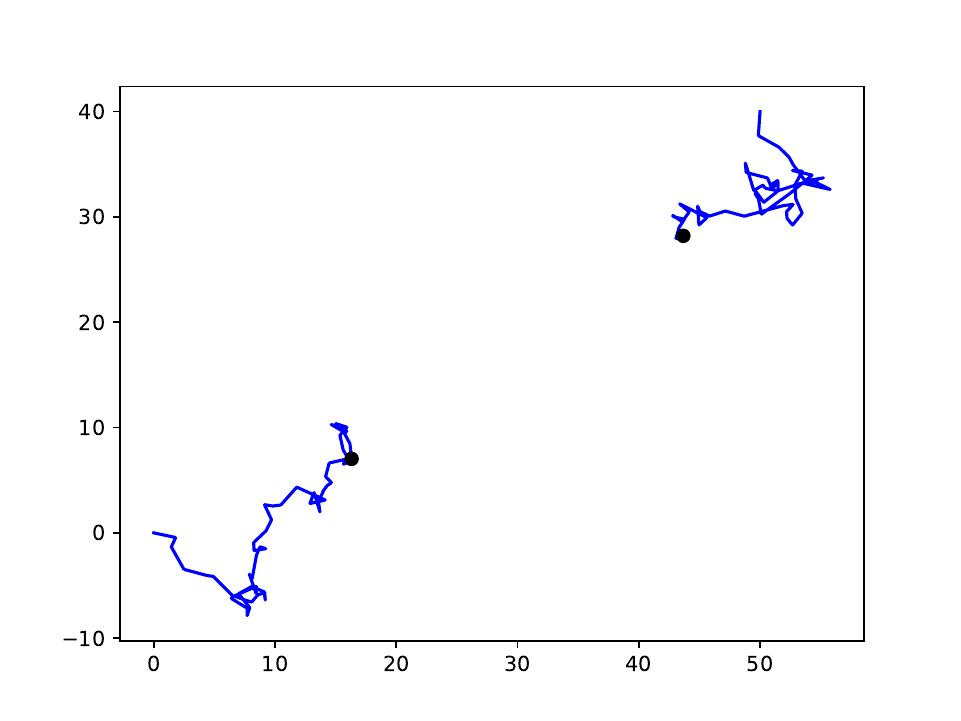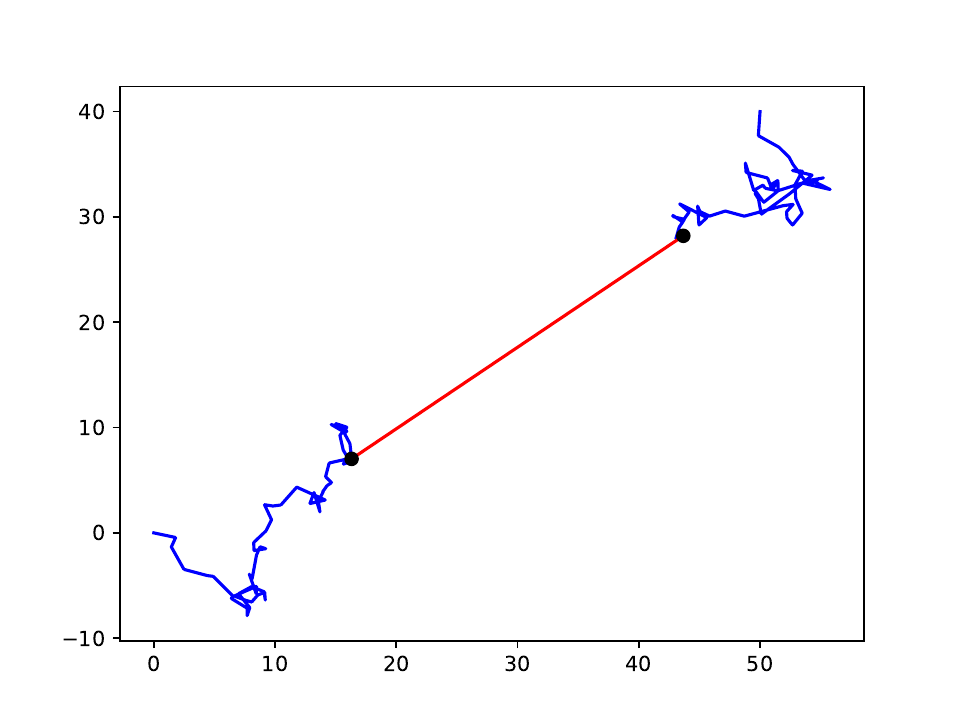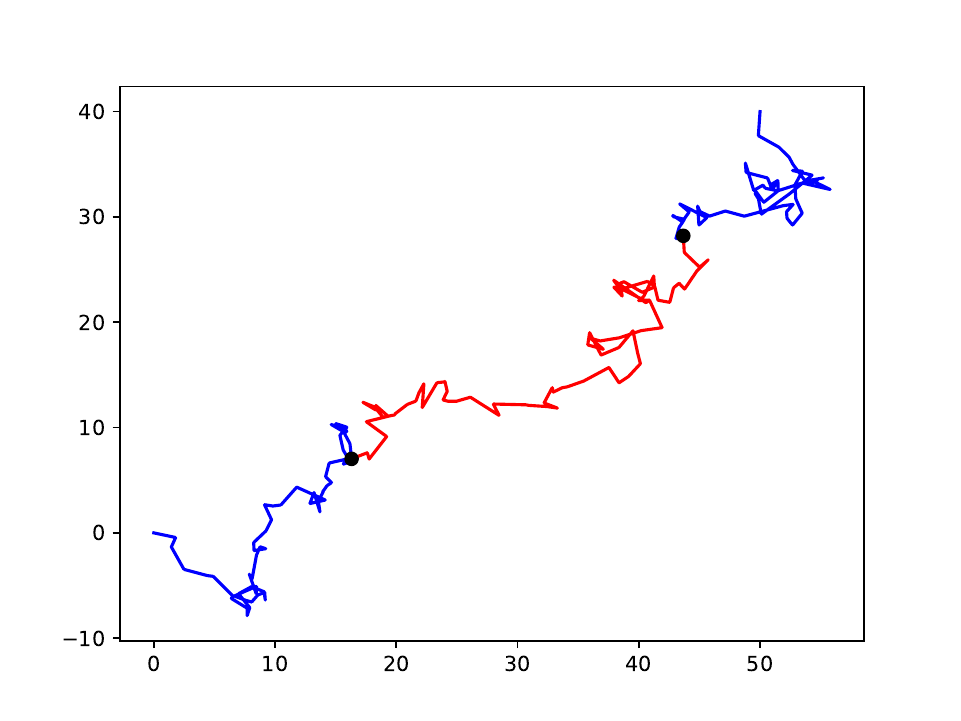
Together with eight other Masters students, we were asked by Statistics Netherlands to find a theoretic solution to this problem. To do this we used a mathematical model called a Brownian bridge to approximate the missing paths. We knew this idea had potential, because these models have been successfully used in ecological research into the way certain animals travel [3]. For example, an ecologist might be interested how many kilometres an animal travels per day, or what its home range is. These properties are similar to some of the properties that are relevant for the ODiN project.

Brownian bridges

The mathematical model we used, the Brownian bridge, is based on a different model called Brownian motion. This is a method to simulate random behavior that is used in many scientific disciplines. It can, for instance, be used to model the collision of gas molecules or price fluctuations of the stock market. It is an example of a random walk, a mathematical process which we can imagine as a person walking, but each step is taken in a random direction. With Brownian motion these steps are completely independent of each other, so future steps are not influenced by the steps taken before. Another property of Brownian motion is that at each point in time, the location of this process has what mathematicians call a normal distribution. This is a relatively simple mathematical tool which is used in all areas of science. This means that Brownian motion, at least from a mathematical point of view, is very easy to work with. A Brownian bridge is, essentially, a Brownian motion whose beginning and end points are fixed, i.e., a random walk where you end up back where you started.

There are four parameters of the Brownian bridge that we need to extract from the data before we can simulate a travel movement.

• The length of time where data is missing, T.
• The distance between the last data point before the gap and the first data point after the gap, d.
• The number of steps we take in our simulation, n.
• The so-called “diffusion coefficient”, σ_m.

The first two, T and d, are easily obtained from the data points you do have. The number of steps n, however, cannot be obtained from the data, as it is a choice to be made at the start of the simulation. The diffusion coefficient σ_m is a positive number that says something about exactly how random the Brownian bridge behaves. If it is close to zero, the path will very likely be a nearly straight line from begin to end points. If it is large, the path is very random, and will probably make many detours before ending up in the end point.

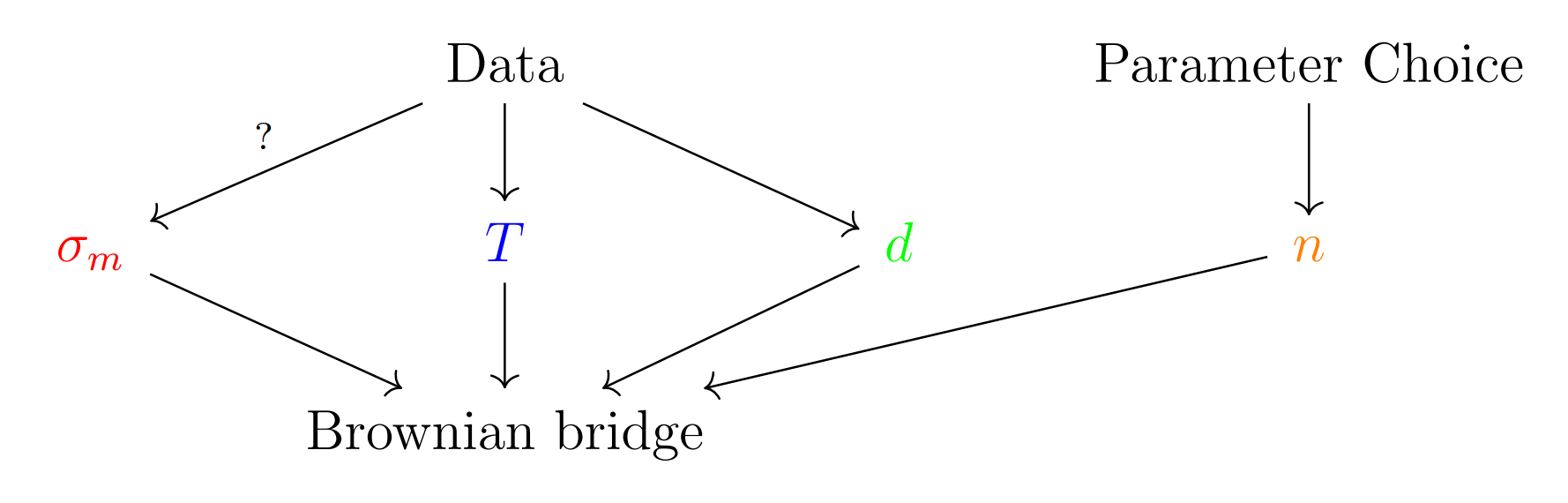
The diffusion coefficient cannot be obtained from the data directly, but we can estimate it. It is a property of the travel movement: an old lady walking her dog will have a very different σ_m than someone on the way to work by car. Since we don’t have data in the gap (that is precisely the problem we are trying to solve), we estimate σ_m using data points just before and / or just after the gap.

To show how this can be done, consider the simple example consisting of seven data points shown in Figure 2 below. To compute σ_m we simulate Brownian bridges with the same unknown parameter σ_m between every other point, here shown in green. Then we consider the skipped points, here shown in blue, to be the realization of those Brownian bridges. Now we can use a statistical tool called maximum likelihood estimation to find the value of σ_m.

We now know how to obtain all four parameters of the Brownian bridge, so we can simulate a travel movement to fit the gap. This is done in Figure 3, where we see that the path seems very ragged. Unless you are very drunk, you are not likely to exhibit this behavior. However, properties like path length which are relevant to the ODiN project, are realistic. Combined with the simplicity of the model, this is a convincing argument to use Brownian motion to simulate travel movements.

However, as we said before, we are interested in certain properties of the travel movement and not the exact path taken. And because Brownian motion is so well-behaving we do not have to simulate the path to compute some of these properties. For one of these, namely the expected path length E[l], there turns out to be a closed formula: an expression in terms of only things we know.

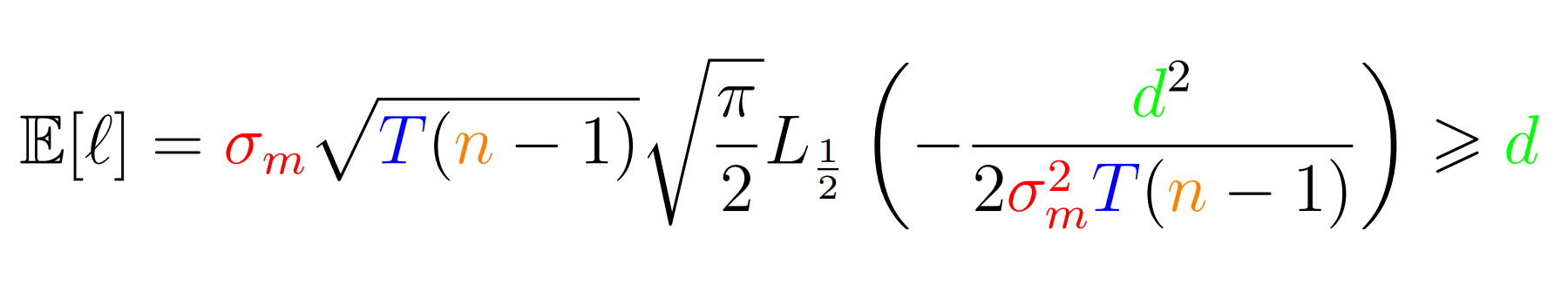
In this expression we can see the so-called Laguerre function L_1/2. While it is a complicated function, the important thing to note is that it is known, and a graphing calculator such as Wolfram Alpha can plot it for you. One of the properties of the formula above is that it is always bounded from below by d. This makes sense: the shortest distance between begin and end points is precisely distance d. Furthermore, if we look at the cases where σ_m is close to zero (very non-random behavior) this expression will be close to d, and if σ_m is large (very random behavior), E[l] will be large as well. This means that this expression behaves just as we expect it will in extreme situations. (Note: the Laguerre function L_1/2 is significantly complicated and it is not at all obvious that its behavior in these limit cases should be how we just described it. You can consult our report [4] if you want to know the mathematical details.)

Results

This formula for the expected path length performed fairly well in a number of simulations. Unsurprisingly, it always does better than the straight line method, as that is quite literally the shortest distance we can take. It is not perfect though, it performs quite differently for different types of movement. Due to privacy concerns we were not able to test it on actual location data, though that is something Statistics Netherlands is going to attempt.

Our method does not work if a participant changes their mode of transportation or stops for a while during a gap. A logical further step would be to improve the model by allowing for a change of vehicle, or even a stop during the travel movement. This has already been successfully implemented in animal movement studies [5]. In these more complicated models an animal may change the intention of their movement, such as going from eating to fleeing from a predator. This, in terms of the model, is similar to a human cycling into town, parking their bike and walking to a shop. In the future these methods might be used to perfectly model human transportation, but at this point in time this is still a bridge to far.

References

[1] Centraal Bureau voor de Statistiek. Totale vervoersprestatie in Nederland (Dutch) [Total travel distance in the Netherlands]. https://www.cbs.nl/nl-nl/cijfers/detail/84687NED#Vervoersprestatie_1. Consulted on July 21, 2022.

[2] Centraal Bureau voor de Statistiek. About CBS. https://www.cbs.nl/en-gb/about-us/organisation. Consulted on July 21, 2022.

[3] J. S. Horne et al. Analyzing animal movements using Brownian bridges. Ecology, 88(9):2354 – 2363, 2007.

[4] L. Dekker, K. Đelić, M. van Dijk et al. Interpolating Location Data with Brownian Motion. https://arxiv.org/abs/2207.01618. Consulted on October 11, 2022.

[5] B. Kranstauber et al. A dynamic brownian bridge movement model to estimate utilization distributions for heterogeneous animal movement Journal of Animal Ecology, 81(4):738–746, 2012.

Article by Tess van Leeuwen and Caspar Meijs (students of the MSc in Mathematical Sciences at Utrecht University, the Netherlands.)